 (r),
where r designates the internal coordinates. Each internal state is called
a channel.
The full wavefunction of the complex
is written as
(r),
where r designates the internal coordinates. Each internal state is called
a channel.
The full wavefunction of the complex
is written as
 (R, r) =
(R, r) = 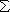 F
(R) x
F
(R) x  (r) (1)
(r) (1)
Substitution of expansion (1) into the Schrödinger equation, premultiplication by one of the internal states, and integration over r gives rise to a set of coupled ordinary differential equations for the expansion coefficients F (R), which are identical to the CC description of molecular scattering.
The general structure of these coupled second-order differential equations is expressed by the matrix equation
Here 1 designates the identity matrix, R is the interparticle distance, and the matrix W(R) is given by
where h designates Planck's constant divided by 2![]() , m is the reduced mass
of the collision system and k2 and l2 designate, respectively, the
(diagonal) matrices of the wavevector and the relative orbital angular
momentum of the collision partners. We have
, m is the reduced mass
of the collision system and k2 and l2 designate, respectively, the
(diagonal) matrices of the wavevector and the relative orbital angular
momentum of the collision partners. We have
where E is the total energy and ei is the internal energy of the ith channel. Also, we have
where li is the relative orbital angular momentum in the ith channel. In Eq. (3) the matrix V(R) is the (full, symmetric) matrix of the coupling potential.
Diagonalization of the W(R) matrix yields the
diagonal matrix of adiabatic wavevectors k(R). The
eigenvectors define the locally adiabatic
states, which are transformations of the internal
states used to expand the scattering wavefunction,  (r).
If C(R) designates the matrix of eigenvectors, column
ordered, then the diagonal matrix of adiabatic energies is defined as
(r).
If C(R) designates the matrix of eigenvectors, column
ordered, then the diagonal matrix of adiabatic energies is defined as
Energies and Wavefuntions
In the adiabatic bender treatment of bound states,[2,3] these adiabatic energies define a set of one-dimensional potentials in R. The wavefunctions and energies of these one-dimensional potentials can be obtained by any standard numerical integration technique, such as the Numerov method.[4] These wavefunctions are the adiabatic-bender approximations to the full wavefunctions of the bend-stretch states of the complex.
Alternatively, the energies and wavefunctions can be obtained by a dual numerical propagation of the the matrix of solutions F(R). Propagation is outward from a value of the interparticle distance R = Rstart, which lies well inside the innermost classical turning point, and inward from R = Rend, which lies well outside the outermost classical turning point. The outwardly and inwardly propagated solution matrices are matched at a distance R = Rmatch. Only at the allowed energies of the system will you be able to match, without discontinuity, both the wavefunction and its first derivative.
Great numerical stability is obtained by propagation of the logarithmic derivative of the solution matrix F(R), namely
rather than the solution matrix itself. The matching condition is [5]
where the subscripts o and i designate, respectively, the logderivative matrices at R = Rmatch obtained from the outward and inward propagations. A good initial estimate of the roots of the determinant in Eq. (8) can be obtained from a prior adiabatic bender calculation.
Equivalently, the energies and wavefunctions can be obtained variationally. Here, each element of the solution matrix, Fi,j(R), is expanded in terms of a set of functions
As in any standard linear variational technique, the energy and eigenfunction of the nth bound state is obtained by diagonalization of the matrix of the full Hamiltonian
in the ![]() (R) basis. The dimensions of this Hamiltonian
matrix are MxNch, where M is the dimensionality of the
(R) basis. The dimensions of this Hamiltonian
matrix are MxNch, where M is the dimensionality of the ![]() (R) basis
and Nch is the number of internal states (channels). In the present implementation
within HibridonTM code, the distributed Gaussian basis of Hamilton
and Light[6] is used, in which
(R) basis
and Nch is the number of internal states (channels). In the present implementation
within HibridonTM code, the distributed Gaussian basis of Hamilton
and Light[6] is used, in which
Coupled States Approximation
Similarly to the treatment of molecular scattering, the Coupled-States approximation can be made for bound states. (This is sometimes called the centrifugal decoupling (CD) approximation [1]). Here, the energies and eigenfunctions refer to a system in which the projection of the total angular momentum along R is assumed to be conserved, so that this projection is a good quantum number.The Hibridon code will calculate bound-state energies if the flag BOUNDC is set .TRUE.
Another, powerful program package for the solution of the close-coupled equations for bound states is the BOUND code developed by J. Hutson.
References
1. J. M. Hutson in Advances in Molecular Vibrations and Collision Dynamics, edited by J. M. Bowman and M. A. Ratner (JAI Press, Greenwich, CT, 1991) 1A, p. 1.
2. S. L. Holmgren, M. Waldman, and W. Klemperer, J. Chem. Phys. 67, 4414 (1977).
3. M. H. Alexander, S. Gregurick, and P. J. Dagdigian, J. Chem. Phys. 101, 2887 (1994).
4. See, for example, J. M. Blatt, J. Comput. Phys. 1, 382 (1967).
5. D. E. Manolopoulos, Ph. D. thesis, University of Cambridge (1988).
6. I. P. Hamilton and J. C. Light, J. Chem. Phys. 84, 306 (1986).
Go to: