Solutions to supplemental problem on Assignment 4, due Oct 9, 2019

1. The four steps of a Stirling cycle are outlined in the figure below (the arrows indicate the direction that the system takes in P,V space)
   
2. w and q for the Stirling engine
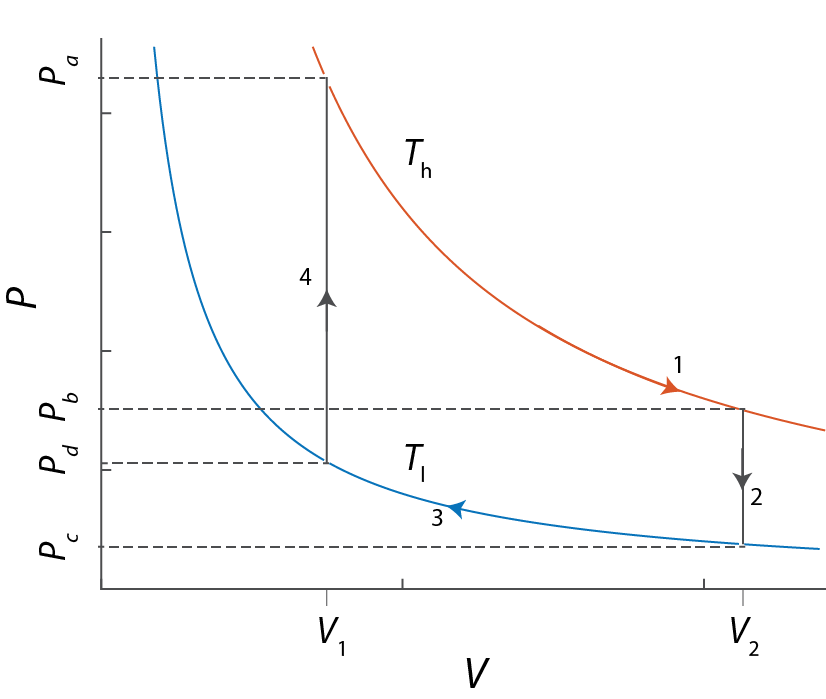
   1. Reversible expansion and compression
      1. The work associated with steps 1 and 3 is $dw=-\int PdV$ where $P$ is the instantaneous pressure of the gas. For an ideal gas, this is $dw = - NRT\ln(V_{final}-V_{initial})$.
      2. For steps 2 and 4, since the volume doesn't change, $w=0$. Then, the First Law tells us that $dU = \delta q$, or $q=C_{\rm V} (T_{final}-T_{initial})$. Also, since Steps 1 and 3 are isothermal, $\Delta U = 0$, so that $q=-w$.
   2. Irreversible expansion and compression
      1. heat flow for each step is formally unchanged, except that the work associated for steps 1 and 3 is different.
      2. For a one-step (irreversible) expansion or compression the work is $dw=-\int P_{ext}dV = -P_{ext}\Delta V$. For the expansion step, the external pressure cannot be greater than $P_b$ (see the above diagram). For the compression step, the external pressure has to be at least equal to $P_d$.

         From the ideal gas law, $P_b=NRT_h/V_2$ and $P_d=NRT_l/V_1$.

      3. The following tables summarize these results (with $\Delta V=V_2-V_1$ and $\Delta T= T_h-T_l$; note that both $\Delta V$ and $\Delta T$ are positive).

   Step	Reversible expansion and compression
   	Work	Heat
   1	$-NRT_h\ln(V_2/V_1)$	$+NRT_h\ln(V_2/V_1)$
   2	0	$-C_{\rm V}\Delta T$
   3	$+NRT_l\ln(V_2/V_1)$	$-NRT_l\ln(V_2/V_1)$
   4	0	$+C_{\rm V}\Delta T$
   $\oint$	$-NR\ln(V_2/V_1)(T_h-T_l)$	$+NR\ln(V_2/V_1)(T_h-T_l)$

   Step	Irreversible
   	Work	Heat
   1	$-NRT_h\Delta V/V_2$	$+NRT_h\Delta V/V_2$
   2	0	$-C_{\rm V}\Delta T$
   3	$+NRT_l\Delta V/V_1$	$-NRT_1\Delta V/V_1$
   4	0	$+C_{\rm V}\Delta T$
   $\oint$	$-NR\Delta V\left (T_h\,/V_2-T_l\,/V_1\right )$	$+NR\Delta V\left (T_h\,/V_2-T_l\,/V_1\right )$

   Note that for the closed cycle to be an engine, we want $\oint \delta w$ to be negative, so that over the complete cycle work is done on the surroundings. For this we need $T_h\,/V_2$ to be greater than $T_l\,/V_1$, or $T_h \gt T_l \,(V_2/V_1)$.

3. If we define the efficiency as the work produced ($\left |\oint \delta w\right|$) divided by the heat absorbed on the expansion step ($q_1$), then we find
   1. If steps 1 and 3 are reversible: $\eta = (T_h-T_l)/T_h$, identical to the Carnot efficiency.
   2. If steps 1 and 3 are single-step: $$\eta = \frac{T_h/V_2-T_l/V_1}{T_h/V_2)}= 1-\frac{T_l}{T_h}\frac{V_2}{V_1}$$

      Obviously if the temperatures and the volumes don't satisfy the inequality $T_h \gt T_l \,(V_2/V_1)$, then the efficiency will turn out to be a negative number (indicative that the whole cycle is not producing work!).

   A more proper definition of the efficiency is the work produced divided by the total heat absorbed ($q_1+q_4$). Since $q_4$ is positive, we see that the efficiency of even the "best" Stirling engine (reversible steps 1 and 3) will be less than that of the Carnot engine.
4. To obtain an efficiency of $\eta = 0.5$ with $T_l=300$, we need $(T_h-T_l)/T_h = (T_h-300)/T_h = 0.5$. Solution gives $T_h=600$.
5. When the demonstration starts up, it shows $T=552^\circ$C$=825$ K, $P=169$ kPa = 1.69$\times 10^5$ Pa, and $V=800$ ml = 8$\times 10^{-4}$ m$^3$. Inserting these numbers into the ideal gas law gives $N=(1.69\times10^5\cdot8\times 10^{-4}) /(8.314 \cdot 825)= 0.020$ mol.