Homework Assignment # 6

Due Wednesday April 3, 2019

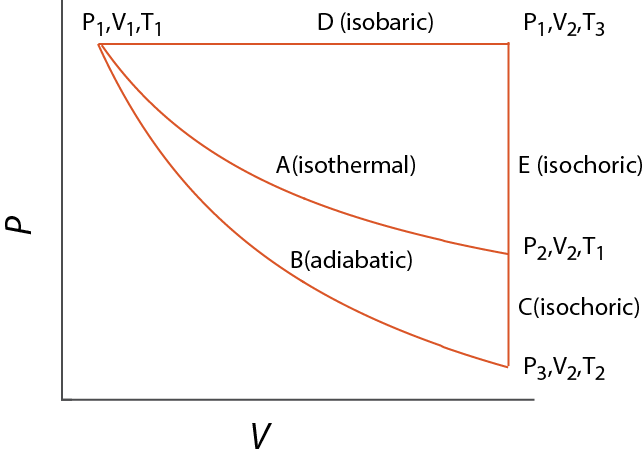
Consider the transformations shown in Fig. 6.3 (reproduced just below) some of these we will discuss in class on 4/3

The following table lists the initial and final pressures, temperatures, and volumes, and well as $\Delta U,\,w,\,q$, and $\Delta S$ for the five reversible transformations shown in the figure above. One mole of a monatomic ideal gas is assumed. The directions of each transformation are indicated in the first column.

step	$P_i$	$V_i$	$T_i$	$P_f$	$V_f$	$T_f$	$\Delta U$	$w_{rev}$	$q_{rev}$	$\Delta S =\int \frac{\delta q_{rev}}{T}$
A (isothermal) $V_1\to V_2$	$P_1$	$V_1$	$T_1$	$\frac{1}{2}P_1$	$2 V_1$	$T_1$	0	$-RT_1 \ln 2$	$+RT_1 \ln 2$	$R \ln 2$
B (adiabatic) $V_1\to V_2$	$P_1$	$V_1$	$T_1$	$2^{-5/3}P_1$	$2V_1$	$\frac{1}{2}^{2/3}T_1$ $=0.630 T_1$	$\frac{3}{2}R\left [\left ( \frac{1}{2}\right )^{2/3}-1\right]T_1$ $=-0.555R T_1$	$-0.555 RT_1$	0	0
C (isochoric) $T_1\to T_2$	$\frac{1}{2}P_1$	$2 V_1$	$T_1$	$2^{-5/3}P_1$	$2V_1$	$T_f=T_2$ $=0.630 T_1$	$\frac{3}{2}R (T_2-T_1)$ $=-0.555 R T_1$	0	$-0.555 R T_1$	$\frac{3}{2} R \int \frac{dT}{T}$ $=\frac{3}{2}R \ln(\frac{1}{2}^{2/3})$ $= - R \ln 2$
D (isobaric) $V_1\to V_2$	$P_1$	$V_1$	$T_1$	$P_1$	$2 V_1$	$2 T_1$	$\frac{3}{2} R T_1$	$-P_1 V_1$ $= -R T_1$	$\frac{5}{2}R T_1$	$R(\frac{3}{2}\int \frac{dt}{T}+ \int \frac{dv}{V})$ $=\frac{5}{2}R \ln 2$
E (isochoric) $T_1\to T_3$	$\frac{1}{2}P_1$	$2 V_1$	$T_1$	$P_1$	$2 V_1$	$2T_1$	$\frac{3}{2}R T_1$	0	$\frac{3}{2}R T_1$	$\frac{3}{2}R \ln 2$

Verify all the entries for steps B and C (we will do this for steps A, D, and E in class).
Consider an isobaric transition that goes from $P_3,V_2$ to $V_1$. What will be the values of $P_f$ and $T_f$ for this transition?
Derive $\Delta U,\,w,\,q$ and $\Delta S$ for (all processes are reversible)
1. An isochoric transition that goes from $P_3,V_2,T_2$ to $P_1,V_2,T_3$.
2. The isobaric transition defined in question 2) above.
3. The cyclic process $P_1,V_1,T_1\to P_1,V_2,T_3\to P_3,V_2,T_2 \to P_1,V_1,T_1$.