In the close coupled treatment of both scattering and photodissociation, the scattering wavefunction
is expanded in a complete set of internal states of the system, usually constructed
as direct products of the internal states of one (or both) fragments, multiplied by
angular functions which describe the rotation of one collision partner about the other.
Let us designate these internal states as  (r),
where r designates the internal coordinates. Each internal state is called
a channel. In the HibridonTM code, the channels are labelled by two integer indices,
a
rotational angular momentum (contained in the array JOUT) and
an additional quantum number or index (contained in the array INDOUT).
(r),
where r designates the internal coordinates. Each internal state is called
a channel. In the HibridonTM code, the channels are labelled by two integer indices,
a
rotational angular momentum (contained in the array JOUT) and
an additional quantum number or index (contained in the array INDOUT).
The full scattering wavefunction is written as
 (R, r) =
(R, r) = 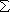 F
(R) x
F
(R) x  (r) (1)
(r) (1)
Substitution of the expansion (1) into the Schrödinger equation, premultiplication by one of the internal states, and integration over r gives rise to a set of coupled ordinary differential equations for the expansion coefficients F (R).
The general structure of these coupled second-order differential equations is expressed by the matrix equation
Here 1 designates the identity matrix, R is the interparticle distance, and the matrix W(R) is given by
where h designates Planck's constant divided by 2![]() , m is the reduced mass
of the collision system and k2 and l2 designate, respectively, the
(diagonal) matrices of the wavevector and the relative orbital angular
momentum of the collision partners. We have
, m is the reduced mass
of the collision system and k2 and l2 designate, respectively, the
(diagonal) matrices of the wavevector and the relative orbital angular
momentum of the collision partners. We have
where E is the total energy and ei is the internal energy of the ith channel. Also, we have
where li is the relative orbital angular momentum in the ith channel. In Eq. (3) the matrix V(R) is the (full, symmetric) matrix of the coupling potential.
Diagonalization of the W(R) matrix yields the
diagonal matrix of adiabatic wavevectors k(R). The
eigenvectors define the locally adiabatic
states, which are transformations of the internal
states used to expand the scattering wavefunction,  (r).
If C(R) designates the matrix of eigenvectors, column
ordered, then the diagonal matrix of adiabatic energies is defined as
(r).
If C(R) designates the matrix of eigenvectors, column
ordered, then the diagonal matrix of adiabatic energies is defined as
One obtains numerically the matrix of solutions F(R) by outward propagation. You start this propagation at a value of the interparticle distance R = Rstart which lies well inside the innermost classical turning point. Once you have propagated F(R) out to a value of R which is so large that the potential V(R) is negligible, compared to the wavevectors k2, you can then match F(R) to the known asymptotic form and obtain the S matrix. This has to be done over and over at many values of the total angular momentum Jtot. In a semiclassical description the total angular momentum corresponds to the impact parameter b. From the S matrix at all these values of Jtot, you can calculate differential and integral cross sections.[2,3]
Cross Sections
Within the CC formulation, the integral cross section for a transition from an initial state i to a final state f is given by
where
ki is the wavevector of the initial state and the sum
runs over:
- all values of the total angular momentum for which the S matrix elements differ from unity.
 You must ensure that the parameter JTOT2 has
been set large enough so that increasing its value will not significantly change
the cross section(s) of interest
You must ensure that the parameter JTOT2 has
been set large enough so that increasing its value will not significantly change
the cross section(s) of interestall values of the orbital angular momentum l allowed by the triangular rule
both values (p = +1 and -1) of the total parity of the scattering wavefunction. The
total parity is related to the important input parameter JLPAR.
 Note
that for full close-coupled determinations of either integral or differential cross sections, the calculations must be carried out for both values of JLPAR.
Note
that for full close-coupled determinations of either integral or differential cross sections, the calculations must be carried out for both values of JLPAR.
Here, the T or transition matrix is defined as
where 1 is the unit matrix. At large Jtot the T matrix goes to zero as the centrifugal potential becomes so large that the colliding particles are kept beyond the range of the interaction potential. This defines the range of total angular momentum for which scattering calculations need be done. The minimum and maximum values of the total angular momentum for which the calculation is done are set by the parameters JTOT1 and JTOT2, respectively.
See Refs. 1 and 2 for an expression for the differential cross section equivalent to Eq. (7).
In general, the CC equations are block diagonal in the overall parity of the scattering wavefunction. To obtain integral and/or differential cross sections it is necessary to carry out calculations for both values of this parity (this is ensured by setting JLPAR=0; see the JLPAR frame for more information).
Equation (7) can be written equivalently in terms of partial cross sections
where the partial cross sections, which can be calculated with the command PARTC, are defined by
In a semiclassical formulation, the integral cross section is written as
in terms of a transition probability which depends on the impact parameter b. The partial cross section is thus equivalent to this semi-classical transition probability, as follows:
Wavefunction and Fluxes
In addition to the determination of cross sections, which depend on the asymptotic form of the expansion coefficients F (R) in Eq. (1), the HibridonTM code allows you determine the R dependence of these coefficients. In addition, one can also determine the flux associated with the scattering and photodissociation wavefunctions, which is a more meaningful physical quantity. For a further discussion see Ref. 4 and 5.)
Methods
The determination of differential and/or integral cross sections involves three steps:
- The development of subroutines to calculate the potential matrix V(R) for a particular collision system.
- Solution of the CC equations to obtain and store the S matrix elements, at both values of the parity index JLPAR.
- The subsequent calculation of differential and/or integral cross sections for the transitions which interest you.
Historically, there have been many algorithms developed to solve these equations. These algorithms can be grouped into two categories[3]:
- Solution-following methods. In these methods you approximate the matrix of solutions F(R) by a power series and then solve Eq. (1) exactly. This is similar in spirit to the usual numerical techniques for solution of ordinary differential equations (Runge-Kutta, Euler, Adams-Moulton).
- Potential-following methods. In these methods the matrix V(R) is approximated by a sequence of constant or linear segments. In these local regions the approximated CC equations can be solved exactly.
In solution-following methods the solution is approximated while the potential is retained exactly. On the other hand, in potential-following methods the potential is approximated but the solution (to this approximate potential) is exact.
No one method is superior at all values of the internuclear separation. Rather, it is best to combine a solution-following method at short-range (R small), where most intermolecular potentials vary rapidly, with a potential-following method at longer range, where the potential varies more slowly but where for many problems the solution can be highly oscillatory. This combination of two methods is called a hybrid integrator.
The HibridonTM hypertext help describes a particular hybrid integrator - the HibridonTM program package.The solution following method used at short range is based on the log-derivative propagator of Johnson,[6-8] as modified recently by Manolopoulos.[9] This propagator is designated LOGD. The potential-following method used at long-range is based on the linear-reference potential of Gordon,[10,11] as modified recently by Alexander and Manolopoulos.[12,13] This propagtor is designated AIRY. The HibridonTM code combines these two fast algorithms (LOGD and AIRY). Both are fast and exceptionally stable. To a large degree the numerical stability is obtained by propagation of the logarithmic derivative of the solution matrix F(R), namely
rather than the solution matrix itself.
Another, powerful program package for the solution of the close coupled equations is the MOLSCAT code developed by S. Green and maintained by J. Hutson.
References
1. A. Arthurs and A. Dalgarno, Proc. Roy. Soc. (London Ser.) A256, 540 (1960).
2. W. A. Lester, Jr., Meth. Comput. Phys. 10, 211 (1971).
3. D. Secrest, in Atom-Molecule Collision Theory: A Guide for the Experimentalist, edited by R. B. Bernstein (Plenum, New York, l979) p. 265.
4. M. H. Alexander, J. Chem. Phys. 95, 8931 (1991); 96, 6672 (1992).
5. D. E. Manolopoulos and M. H. Alexander, J. Chem. Phys. 97, 2527 (1992); M. H. Alexander, C. Rist, and D. E. Manolopoulos, J. Chem. Phys. 97, 4836 (1992).
6. B. R. Johnson, J. Comput. Phys. 13, 445 (1973).
7. B. R. Johnson, Proceedings of the NRCC Workshop on Algorithms and Computer Codes in Atomic and Molecular Scattering Theory, edited by L. D. Thomas (Lawrence Berkeley Laboratory, CA Report LBL-9501 l979) pp. 86-92 (Vol. I) and p. 52 (Vol. II).
8. F. Mrugala and D. Secrest, J. Chem. Phys. 78, 5954 (1983).
9. D. E. Manolopoulos, J. Chem. Phys. 85, 6425 (1986).
10. R. G. Gordon, Meth. Comput. Phys. 10, 81 (1971).
11. R. G. Gordon, J. Chem. Phys. 51, 14 (1969).
12. M. H. Alexander, J. Chem. Phys. 81, 4510 (1984).
13. M. H. Alexander and D. E. Manolopoulos, J. Chem. Phys. 86, 2044 (1987).
Go to: