- Determine the temperature of the boiling point of benzene at $P=2$ atm and $P=500$ torr The temperature of boiling is given by $1/T_{vap}= (17.63-\ln P)/3884$. We find, for $P$=500 and 760 torr, $1/T_{vap}$=2.9391e-03 and 2.8313e-03, or $T_{vap}=$ 340.2K and 353.2K.
- With the answers to part (a), determine $\Delta H_{vap}$ of benzene (kJ/mol). Here we can use the Clausius-Clapeyron equation $\ln(P_2/P_1)=-(\Delta H/R)(1/T_2 - 1/T_1)$ which becomes $\ln(760/500)=-(\Delta H/8.314)\times(0.0028313-0.0029391)$ Solving for $\Delta H$ gives $\Delta H$=32.29 kJ/mol.
| quantity | CH3OH(l) | CH3OH(g) |
|---|---|---|
| ΔHvap (kJ/mol) | A exp(–α T/Tc)(1–T/Tc)β | |
| CP (J/mol·K) | 80.3 | 46.0 |
| So (J/mol·K) | 127.2 | 239.9 |
Where the constants are A=45.3 kJ/mol, α=–0.31, β = 0.4241, and Tc=512.6 K.
- PLot the molar heat of vaporization of methanol (kJ/mol) from 300K to 400K.
Here is the plot, energies in kJ/mol

- Assuming that the entropies are unchanged over then range 300 to 400 K, determine the boiling point of methanol at 1 atm pressure. Hint: You can
look this up online. You should get a value within 5 % of the online value.
We know that $$\Delta G_{vap} = \Delta H_{vap} - T \Delta S_{vap}$$ $\Delta H_{vap}$ was shown in the previous plot, and here we assume that $\Delta S_{vap}= S(g)-S(l)\approx S^{(o)}(g)-S^{(o)}(l)=239.9-127.2 = 112.7$ J/mol$\cdot$K. A plot of $\Delta G_{vap}$ over the temperature range 300--350K is the blue curve in the figure.
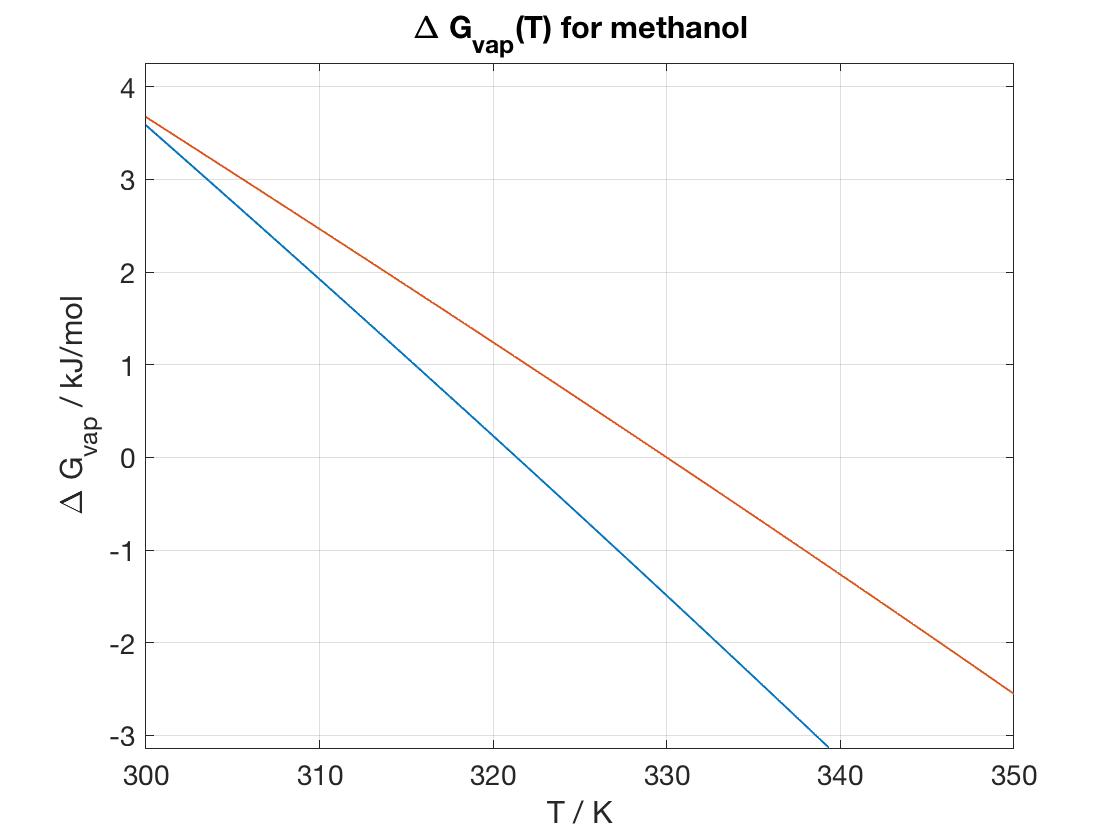
The root (the value of T where $\Delta G =0$) can be estimated from the plot as 321.5 K. The literature value is 337.8 K - Now assume that the entropies vary with temperature as dS/dT = CP/T. Determine a revised value of the boiling point. In fact, the entropies do change with temperature. We know $(\partial S/\partial T)=C_P/T$, so that $S(T)=S^{(o)}+C_P \ln (T/298)$, thus \begin{eqnarray*}\Delta S_{vap}&=& S(g)-S(l) = S^{(o)}(g)-S^{(o)}(l) + [C_P(g)-C_P(l)]\ln(T/298)=\Delta S^{(o)}+\Delta C_P \ln(T/298)\nonumber \\ &=& 112.7 - 44.3 \ln(T/298) \end{eqnarray*} A plot of this is the red curve in the above figure. The estimated root is 330 K, much closer to the literature value
- Why does the value you obtain in part (c) differ from the experimental value? We have assumed the specific heats are constant. Correcting for this would lead to slightly better agreement.